Electronique de puissance
L’électronique de puissance est une branche de l’électronique qui a pour objet
la conversion statique de l’énergie électrique.
La conversion statique est réalisée par des convertisseurs statiques qui
transforment l’énergie électrique disponible en une forme adaptée à
l’alimentation d’une charge bien déterminée.
Différents types de convertisseurs statiques
Selon le réseau disponible et le besoin de la charge, on distingue différents type de convertisseurs :
convertisseur alternatif = continu : redresseur
convertisseur continu = alternatif : onduleur
convertisseur continu contenu = hacheur
convertisseur alternatif = alternatif (à fréquence fixe) gradateur
convertisseur alternatif (f1) = alternatif (f2) cyclo convertisseur
le redresseur convertit l’énergie alternative disponible en énergie continue.
Diode de puissance
C’est un interrupteur unidirectionnel en courant non commandable ni à la fermeture ni à l’ouverture : Blocage et amorçage naturel.
Une diode se comporte comme un interrupteur parfait dont les commutations sont exclusivement spontanées :
il est fermé tant que le courant qui le traverse est positif
il est ouvert tant que la tension à ses bornes est négative
Thyristor
C’est un interrupteur unidirectionnel en courant commandable à la fermeture :
VAK> 0 et pas d’impulsion sur la gâchette : thyristor bloqué
(thyristor amorçable)
VAK > 0 et on applique un courant de gâchette iG positif de valeur suffisante :
thyristor passant (thyristor amorcé)
Une fois il est passant, le thyristor ne s’ouvre que lorsque le courant qui le traverse s’annule.
Le thyristor est bloqué et VAK < 0 et on applique une impulsion de commande : thyristor reste bloqué.
Transistor bipolaire de puissance
En électronique de puissance, les transistors fonctionnent en régime de commutation tandis que le fonctionnement linéaire est plutôt utilisé en amplification de signaux.
Le transistor bipolaire joue le rôle d’interrupteur unidirectionnel en courant et tension commandable à la fermeture et à l’ouverture par le biais du courant de base iB :
Transistor bloqué : état obtenu en annulant le courant de base iB( 𝑖𝐵 = 0) ce qui induit un courant de collecteur nul( 𝑖𝑐 = 0 ) et une tension VCE non fixée. L’équivalent est un commutateur ouvert
Transistor saturé : ici, le courant iB est tel que le transistor impose une tension VCE nulle tandis que le courant ic atteint une valeur limite dite de saturation icsat. L’équivalent est un commutateur fermé
Transistor MOSFET de puissance
Le transistor MOSFET est un interrupteur commandé à la fermeture et à l’ouverture par la tension VGS :
VGS = 0 annule le courant iD ( 𝑖𝐷 = 0) : transistor bloqu
VGS ≥ VGsat permet au courant iD de se croitre : transistor saturé
Transistor IGBT (Insulated Gate Bipolor Transistor)
Le transistor IGBT (Insulated Gate Bipolar Transistor) est l’association d’un transistor bipolaire (collecteur et émetteur) et d’un transistor MOSFET. Il associe les performances en courant entre collecteur et émetteur (la faible chute de tension collecteur émetteur est de 0,1 V) et la commande en tension par sa grille qui nécessite un courant permanent quasiment nul. Il est commandé à la fermeture et à l’ouverture par la tension VGE.
EXERCICE CORRIGE
Le pont ci-dessus alimente
l'induit d'un moteur à courant continu à excitation indépendante et constante
et dont la résistance de l'induit est de 0,5 W.
La f.é.m est égale à 180V quand la fréquence de
rotation est de 1250 tr.min-1.
Le courant dans le moteur est parfaitement lissé
par une inductance pure et son intensité a pour valeur I = 10 A.
On applique à l'entrée du pont
une tension sinusoïdale de valeur efficace 220 V et de fréquence 50 Hz.
Les thyristors reçoivent des
impulsions de gâchette aux instants (t0 + kT/2) (k = 0,1,
2,............)
1.
Sur l'axe "horizontal" du chronogramme
de v, faire apparaître les indications 2,5 ms, 10 ms, 20 ms "en dessous
" de l'axe et p /4
rad, p rad,
2 p rad
au-dessus de l'axe.
2.
En s'aidant du chronogramme figurant sur la page
4, écrire l'expression de la tension v appliquée à l'entrée du pont sous la
forme :
v = Vmax sin (w t + j ) en donnant les valeurs de Vmax, w et j. (l'expression trouvée ne devra comporter que la seule lettre t ) .
v = Vmax sin (w t + j ) en donnant les valeurs de Vmax, w et j. (l'expression trouvée ne devra comporter que la seule lettre t ) .
3.
En s'aidant des chronogrammes figurant à la page
4 :
3.1. Passer
en trait gras sur chacun des
schémas n°1, 2, 3, 4, le "chemin
emprunté" par le courant sur l'intervalle de temps indiqué sous chacun
d'eux, en remplaçant par un interrupteur fermé les éléments passants et par un
interrupteur ouvert les éléments bloqués. Indiquer le sens réel du courant.
3.2. Indiquer
en bas de la page 4, à l'emplacement prévu,
1.2.1.
le signe de la puissance instantanée reçue par
la charge.
1.2.2.
le nom de la phase (écrire "RL" : pour
phase de roue libre et "Alim" pour phase d'alimentation de la charge.
IL : intensité
du courant dans la ligne.
i1 : intensité du courant dans le thyristor T1.
iD1 :
intensité du courant dans la diode D1.
3.4. Sur
le schéma n°5 indiquer les connexions à réaliser pour visualiser simultanément
:
- sur la voie 1 : l'intensité du
courant i3 dans le thyristor T3.
- sur la voie 2 : l'intensité iL
du courant dans la ligne.
On supposera que les deux voies de l'oscilloscope peuvent être
inversées et on fera apparaître au besoin sur le schéma des résistances de
visualisation.
3.5. Exprimer
à l'aide d'une intégrale la valeur moyenne <u> de u quand q = wt0= 45°. L'expression trouvée ne
comportera que la seule variable angulaire a , les autres termes seront remplacées par leurs valeurs
(en particulier, les bornes de l'intervalle d'intégration).
3.6. Calculer
la valeur efficace de l'intensité du courant dans le thyristor T1.
4 Par des considérations géométriques sur l'allure
de u, donner les valeurs de q
pour lesquelles :
4.1. <u>
est maximale ; préciser quelle est alors la valeur de <u>.
4.2. <u>
est minimale ; préciser quelle est alors la valeur de <u>.
Pour le calcul de
<u>, on pourra s'aider de la formule :
5.
5.1. Exprimer
u en fonction de L, de i , de E et de R.
5.2. En
déduire la valeur moyenne <u> de u
en fonction des paramètres de la charge.
5.3. Calculer
la f.é.m E pour q =
45°.
5.4. Quelle
est pour cette valeur de q
(45°) la fréquence de rotation du moteur ?
6.
Donner un avantage et un inconvénient du pont
mixte sur le pont tout thyristors.
SLOLUTION
1. Voir
la page des oscillogrammes
2. La
tension v est une tension sinusoïdale et
a donc pour expression ;
v = Vmax sin ( w t + j )On
a :
j = 0 puisque la sinusoïde passe par l'origine des axes.
w = 2 p
f = 100 p
rad.s-1
Vmax = 220 Ö2 V
d'où :
v = 220 Ö2 sin
100 p t
3
3.1. Voir
plus bas
3.2. Voir
plus bas
3.3. Voir
plus bas
3.4. Voir
plus bas
3.5
3.6
4
4.1. <u>
est maximale pour q = 0 et sa valeur est alors <u> = 198 V
4.2. <u>
est minimale pour q = p rad et sa valeur est alors <u> = 0 V
5.
5.1. (en valeurs instantanées)
52. ce
qui donne
<u>=
E + R<i> puisque Ldi/dt
est nulle du fait que l'intensité i est constante.
5.3. Pour
q = p /4,
on a :
E = <u> - R<i>
E =169 - 0,5x10
E = 164 V
5.
La
fréquence de rotation étant de 1250 tr/min quand la f.e.m est de 180 Vet puisqu'à
excitation constante la f.e.m d'un moteur est proportionnelle à sa fréquence de
rotation, on peut écrire
EXERCICE2:

1- Le pont est alimenté avec une tension sinusoïdale v de fréquence 50 Hz. Représenter en concordance de temps la tension u(t) et la tension v(t). Préciser les intervalles de conduction de chaque thyristor et de chaque diode sur une période.
2- Calculer la valeur efficace de la tension v.
3- La résistance de l’induit du moteur est R = 0,4 Ω. Calculer la f.e.m. du moteur. En déduire la puissance électromagnétique Pem du moteur. Calculer la puissance absorbée par l'induit du moteur.
4- La charge du moteur variant, le moment Tem de son couple électromagnétique est doublé. Que devient la f.e.m. du moteur ? En déduire la vitesse de rotation. Commentaire ?
SOLUTION
Un pont mixte monophasé alimente un moteur à courant continu à excitation indépendante et constante. Il délivre une tension u de valeur moyenne < u > = 169 V, l'angle θ de retard à l'amorçage des thyristors étant réglé à 45°. Le courant dans le moteur est parfaitement lissé par une bobine de résistance interne r = 0,1 Ω. Son intensité I est égale à 25 A. La vitesse de rotation du moteur est de 1800 tours par minute.
1- Le pont est alimenté avec une tension sinusoïdale v de fréquence 50 Hz. Représenter en concordance de temps la tension u(t) et la tension v(t). Préciser les intervalles de conduction de chaque thyristor et de chaque diode sur une période.
2- Calculer la valeur efficace de la tension v.
3- La résistance de l’induit du moteur est R = 0,4 Ω. Calculer la f.e.m. du moteur.
E = < u > - (r + R)I =169 – (0,1+0,4)×25 = 156,5 V En déduire la puissance électromagnétique Pem du moteur.
EI = 156,5×25 = 3,91 kW Calculer la puissance absorbée par l'induit du moteur
.I – rI² = 4,16 kW Autre méthode : Pem + RI² = 4,16 kW
4- La charge du moteur variant, le moment Tem de son couple électromagnétique est doublé.
Que devient la f.e.m. du moteur ? L’excitation du moteur est constante donc le couple électromagnétique est proportionnel au courant d’induit.
I = 2×25 = 50 A E = < u > - (r + R)I = 169 – (0,1+0,4)×50 = 144 V En déduire la vitesse de rotation. Commentaire ?
L’excitation du moteur étant constante, la vitesse de rotation est proportionnelle à la fem. 1800×144 / 156,5 = 1660 tr/min Pour une charge doublée, la vitesse de rotation chute de 8 %.
La vitesse de rotation est peu sensible à la charge
EXERCICE3:
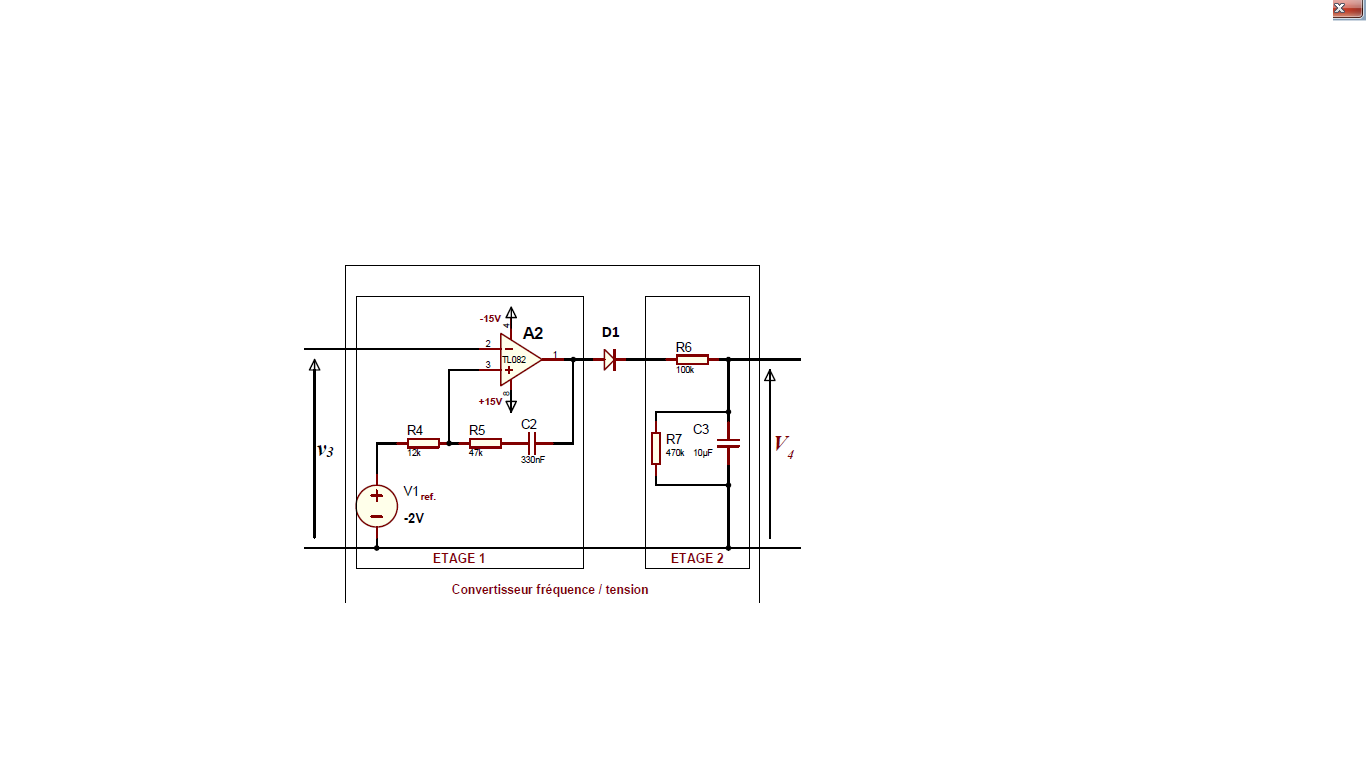
Ce bloc (Figure 17) est constitué de deux étages « étage 1 » et « étage 2 ». La tension V4 doit être en
principe une tension continue qui varie proportionnellement à la fréquence des impulsions de v3 , donc à la vitesse du vent.
Répondre aux questions Q33, Q34 et Q35 suivantes en précisant la bonne réponse (a ou b ou c)
Q33: L’étage 1 est :
a) un multivibrateur astable ;
b) un amplificateur inverseur ;
c) un monostable.
Q34: Le rôle de la diode D1 est de:
a) protéger l’amplificateur Opérationnel A2 ;
b) modifier la constante de temps de l’étage 2 ;
c) bloquer « - VSAT ».
Q35: L’étage 2 est :
a) un filtre passe-bas ;
b) un filtre passe-haut ;
c) un filtre passe-bande.
Q36: On donne :V4 = 0,095 x f et f = 3,34 xVv ;
avec f : fréquence en hertz (Hz) des impulsions de v3 et Vv : vitesse du vent en metre par seconde (m/s).
Calculer les valeurs (V41, V42) de la tension continue V4 :
V41 : Valeur de la tension V4 pour une vitesse du vent égale à 72 km/h ;
V42 : Valeur de la tension V4 pour une vitesse du vent égale à 54 km/h.
SOLUTION
Q33: c) : un monostable.
Q34: c) : Bloquer « - VSAT ».
Q35: a) : un filtre passe-bas.
V41 à 72 km/h : 72/3,6 = 20 m/s
V41 = 0,095x3,34x20 = 6,34V.
V42 à 54 km/h : 54/3,6 = 15 m/s
V42 = 0,095x3,34x15 = 4,75V.
EXERCICE4:
T1 : Transformateur 230v / 2 X 15v - 1,8VA - Type EI 30/15,5;
PD1 : Pont de diodes série RB-1,5A boîtier rond ;
F1 : Fusible temporisé F1T/FST 100 mA.
On suppose que le transformateur est parfait :
1.Comment sont montés les enroulements au secondaire du transformateur
2. Calculer le courant nominal I1 au primaire du transformateur.
3. Calculer le courant nominal I2 au secondaire du transformateur.
4. Calculer le courant nominal Ib dans un enroulement du secondaire.
5. Calculer le rapport de transformation m
solution
1. Les enroulements sont montés en parallèle
2. Courant au primaire du transformateur I1
S=1,8VA=U1.I1 I1=S/U1=8,2mA
3. Calcul du courant au secondaire du transformateur I2
I2=S/U2 I2=1,8/15=120mA
4. Calcul du courant dans un enroulement du transformateur Ib
Ib=I2/2=60mA
5. Calcul du rapport de transformation m
m=U2/U1 m=15/230=0,065
La tension vT à la sortie du capteur est une image de la température.
Cette tension, à faible variation, est appliquée à un filtre R1C1
passif de type passe-bas du 1er ordre
On admet que le signal vT(t) est composé d’une composante continue VT et de perturbations du secteur vPe(t)
qu’on peut considérer sinusoïdales à fréquence constante (vPe(t) = VPeMAX sin (ωt)) ce qui nous permet alors
l’emploi de la notation complexe (VP).
1.On demande d’exprimer VPs en fonction de VPe et des éléments du montage R1 et C1, en déduire
la fonction de transfert T= VPs / VPe
2.Mettre T sous la forme T=1/1+jω/ω0 exprimer ω0 en fonction de R1 et C1.
3.Pour C1= 3,3 μF, calculer la valeur de R1 pour avoir une fréquence de coupure f0= 5Hz.
SOLUTION
1.T = VPs / VPe.= 1/1+jR1C1ω
2.VPs / VPe=1/1+jω/ω0 avec ω0=1/R1C1
3.R1= 1/(2.π.5.3,3.10-6) = 106 /33.π = 9,6 KΩ R1= 9,6 KΩ
R1=9,6 kΩ















Aucun commentaire:
Enregistrer un commentaire