I /
Exercice 1:
Montage amplificateur
On considère le montage amplificateur suivant:
1°) Sans faire de calculs, cet amplificateur est-il inverseur ou non inverseur et pourquoi?
2°) ue est un signal sinusoïdal d'amplitude 0,8v, on désire pour us un signal d'amplitude 5v. Calculer l'amplification en tension Av.
3°) Calculer le gain en tension Gv. 4°) Calculer les résistance R1 et R2 afin que le courant efficace i soit de 0,1mA.
SOLUTION
1°) Ce montage est un amplificateur non inverseur car le signal d’entrée à traiter Ue est appliqué sur l’entrée non inverseuse de l’AIL E+.
2°) Av = Us /Ue = 5/0,8 = 6,25
3°) G(dB) = 20.log(Av) = 20log(6,25) = 15,9dB
4°) R1 = Ueeff / Ieff = (0,8/1,414)/0,1.10-3 = 5,65kΩ Aussi,
R1 + R2 = Useff / Ieff = (5/1,414)/(0,1.10-3 ) = 35,35kΩ
Donc R2 = (35,35 – 5,65).103 = 29,7kΩ
Exercice 2:
Dans le montage considéré, l'amplificateur opérationnel est supposé idéal: résistance d'entrée infinie (courant d'entrée nul) et amplification différentielle en boucle ouverte infinie (tension différentielle nulle). Le voltmètre est utilisé sur le calibre 1v continu. On donne Ue = 1v et R0 = 10K. Ω
1°) Exprimer en fonction de Ue et R0 l'intensité I circulant dans la résistance R0.
2°) Exprimer en fonction de Ue, R0 et Rx la tension Us aux bornes du voltmètre.
3°) Tracer la courbe représentative Us = f(Rx) Echelles: 1K Ω /cm ; 0,1v/cm
4°) Déduire de la question précédente la valeur maximale de la résistance Rx.
SOLUTION
Montage Amplificateur inverseur :
1°) I = Ue/R0
2°) Us = - (Rx/R0).Ue
3°) Usmax = -1v
4°) Rxmax = 10kΩ
Exercice 3:
Dans le montage qui suit, ue est un signal sinusoïdal d'amplitude 0,5v et us un signal d'amplitude 6v. Les amplificateurs opérationnels sont considérés comme réels.
1°) Calculer l'amplification en tension Av du dispositif.
2°) Calculer le gain en tension Gv.
3°) Calculer la valeur de R2 pour R1 = 2KΩ
4°) Représenter sur un même graphe ue et us.
5°) La résistance R3 sert à compenser les écarts entre les courants d'entrée dans l'amplificateur opérationnel. Pour ce montage, on démontre que R3 = R1 // R2. Calculer R3.
SOLUTION
Montage Amplificateur inverseur précédé d’un montage suiveur :
1°) Av = Vs/Ve = - 6/0,5 = - 12
2°) G(dB) = 20.log(Av) = 20log12 = 15,9dB
3°) Av = R2/R1 = - 12 donc –R2 = -12.R1 alors R2 = 24kΩ
4°) Non corrigée.
5°) R3 = (R1.R2) / (R1+R2) = (2x24) / (2+24) = 48/26 = 1,85 kΩ
Exercice 4:
On considère le montage ci-contre. Calculer l'intensité du courant I. On donne:
E = 10v, R1 = R2 = 10KΩ et R3 = 5KΩ Réponses : 2mA; -2mA; 1mA; -1mA.
I = (E/R3)x[R2/(R1+R2)] = (10/5)x[10/(10+10)] = 1mA
Exercice 5
Dans le montage ci-contre, on donne: V1 = -6v; V2 = -5v; R1 = R2 = R3 = 1K Ω
Quelle est l'intensité du courant I ?
SOLUTION
Montage comparateur simple :
Réponses: -14mA; 14mA; -1mA; 1mA.
E = V2 – V1 = - 5 – (-6) = 1v >0 Alors Us = +Vsat = 14v I = 14/1.103 =14mA
Exercice 6
Dans le montage ci-contre, quelle est la valeur de la tension de sortie Vs ?
On donne: Ve = 1v; R1 = 1KΩ; R2 = 10KΩ
Réponses: -10v; 10v; -11v; 11v.
Montage Amplificateur inverseur :
Vs = - (R2/R1).Ve = - (10/1).1 = - 10v
Exercice 7
Dans le montage ci-contre, quelle est la valeur de la tension de sortie U2 ?
On donne: U1 = 5v
R1 = R3 = 1KΩ; R2 = 4KΩ Réponses: 20v; 25v; 12v; 0v.
SOLUTION
Montage Amplificateur non inverseur :
U2 = (1+R2/R1).U1 = (1+4/1).5 = 25v
L’AIL est saturé, la tension U2 ne peut pas dépasser la tension Usat = 12v. Par conséquent, la tension U2 vaut 12v.
EXERCICE 8
Sachant que
R1 = 10kΩ, R2 = 20kΩ et R = 20kΩ,
calculez la tension de sortie Vo dans les deux cas suivants :
cas 1 : Vi1 = +5V et Vi2 = +1V .
cas 2 : Vi1 = +12V et Vi2 = +3V .
Tout d’abord, il faut remarquer que l’ampli-op est aliment´e avec les tensions ±15V . Cela veut dire que le maximum que l’on peut mesurer a` sa sortie est la tension de saturation Vsat ´egale a` environ 80% de la tension d’alimentation, c’est-`a-dire ±15V × 80% = ±12
cas 1 : La tension de sortie de l’ampli-op est:
Vo = − R/R1 Vi1 − R R2 Vi2
Vo = − 20kΩ /10kΩ (5V ) − 20kΩ /20kΩ (1V )
Vo = −11V
Cette tension est celle réellement muser´ee la sortie de l’ampli-op. Elle est donc acceptable.
cas 2 : La tension de sortie de l’ampli-op est:
Vo = − R /R1 Vi1 − R/ R2 Vi2
Vo = − 20kΩ/10kΩ (12V ) − 20kΩ/ 20kΩ (3V )
Vo = −27V
Cette tension ne peut pas être muser´ee a` la sortie de l’ampli-op. On va plutˆot mesurer la tension de saturation de −12V car c’est le maximum que l’on puisse obtenir. Ainsi, il faut faire attention a` ne pas additionner des tensions dont le résultat peut mettre l’ampli-op en saturation car le résultat sera fausse
EXERCICE 9
Soit un amplificateur de courant. Trouvez le gain en courant io/ii de l’amplificateur en fonction des résistances
SOLUTION
En observant la figure et en se basant sur les ´equations de base d’un ampli-op, on sait que :
V + = V − Comme V + = 0,
alors on en d´eduit que : V + = V − = 0.
De plus, puisque V − = Vx, alors on a aussi Vx = 0.
Le courant qui entre dans la borne − est nul par définition. On en deduit que le courant qui traverse
la résistance R1 est le même que celui qui traverse la résistance R2. Maintenant, en se basant sur la
figure, on peut écrire les équations suivantes:
ii = io + i
VR2 + VR4 = 0 car les deux bouts de la branche sont au potentiel Z´ero
(potentiels x et z)
iR2 + iR4 = 0
i1R2 = −iR
i1R2 = −(ii − io)R4
ii [R2 + R4] = ioR
ii = io (R4/ R2 + R4)
io /ii = 1 + R2 /R4
II/
EXERCICE1
Le dispositif de séchage est constitué d’un turbo ventilateur et des résistances chauffantes identiques Rch afin de fournir de l’air chaud dont la température est comprise entre 40°C et 70°C.
Son schéma de principe est le suivant :
Les amplificateurs opérationnels sont supposés parfaits avec ±Vsat= ± VCC= ± 12 V;
- Le capteur de température est une thermistance à coefficient de température négatif (CTN).
Sa résistance varie en fonction de la température selon la loi suivante :
𝐑=𝐑𝟎.𝐞𝛃 (𝟏/𝐓 − 𝟏/𝐓𝟎)
T et T0 sont en degré Kelvin (°K);
R0= 10 KΩ la résistance à la température T0=298°K;
e : base du logarithme népérien ;
β =3977 °K est un coefficient donné par le fabriquant.
On rappelle que la température en degré Kelvin T(°K) = T(°C) + 273.
Bloc1:
Pont de Wheatstone
- Déterminer la valeur de R4 (CTN) qui correspondant à 70 °C.
- Donner l’expression de VB en fonction de VCC , R3 et R4.
Bloc2
Amplificateur de différence
1- Donner l’expression de Vs1 en fonction de VA, R5 et R6
- Donner l’expression de Vs2 en fonction de Vs1,VB, R7 et R8. [2 pts]
- Sachant que :
𝐕𝐒𝟐=𝐕B( 𝟏+𝐑𝟖/𝐑𝟕) −𝐕𝐀 𝟏(𝐑𝟔/𝐑𝟓) 𝐑𝟖/𝐑𝟕
R5 = R6 = R7 = R8 = 10 KΩ
UAB = -1,84 V à 40°C
UAB = - 4,24 V à 70°C
Déterminer VS2 en fonction de UAB , en déduire alors les valeurs de VS2 correspondantes à 40°C et à 70°C.
Bloc3:
- Quelle est la fonction de ce bloc ?
- Sachant que les valeurs des tensions de seuil : VSB (seuil bas)= 3,68 V et
VSH (seuil haut) =8,48 V
tracer la fonction de transfert VS3 =f(VS2) ; en déduire alors la caractéristique VS3 =f(T), la température T est en °C.
SOLUTION
Bloc1
Pont de Wheatstone
- R4=1,74 KΩ
- 𝐕𝐁=𝐕𝐂𝐂 𝐑𝟑/𝐑𝟑+𝐑𝟒
Bloc2
Amplificateur de différence
- 𝐕𝐒𝟏=𝐕𝐀 (𝟏+𝐑𝟔/𝐑𝟓)
- 𝐕𝐒𝟐=𝐕𝐁( 𝟏+𝐑𝟖/𝐑𝟕) −𝐕𝐒𝟏𝐑𝟖/𝐑𝟕
- VS2= -2xUAB = + 3,68 V à 40°C et VS2= -2xUAB = + 8,48 V à 70°C
Bloc3
-Comparaison à deux seuils avec inversion/ mise en forme / comparaison à trigger inverseur
2-
3
EXERCICE2
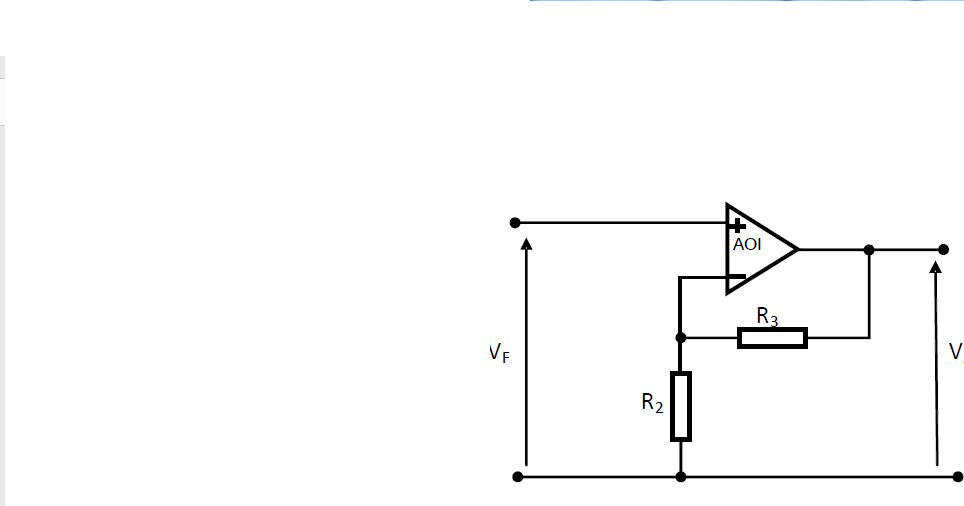
Pour cela on utilise un amplificateur linéaire à base d’amplificateur opérationnel
1-Quel serait alors le module (valeur numérique) de l’amplification ? A=VA/VF
2- Exprimer A en fonction de R2 et R3.
3- Pour R1 = (R2//R3)= 10KΩ (compensation des courants d’offset), calculer les valeurs de R2 et R3.
SOLUTION
L’amplification
1.A = VA/VF est de 10 =(5V/500mV).
2. VF= VA . R2/(R2+R3) ; A= VA/VF = (1+R3/R2)
A = VA / VF = (1+R3/R2)
3. D’une part nous avons A=10=> R3= 9.R2, d’autre part R1= R2.R3/(R2+R3) = 10 kΩ
R2 = 11,11 kΩ ; R3 = 100 kΩ
EXERCICE4
Les amplificateurs opérationnels AO1 à AO3 sont supposés parfaits et sont alimentés entre
VCC=12 V et 0 V.
Les diodes D1 à D3 sont supposées idéales.
Le bloc " Jauges de contrainte " délivre une tension U1 proportionnelle à la masse M : U1=k.M (k : sensibilité,k= 5 mV/g ).
Déterminer les masses minimale (M min) et maximale (M max) pour une brioche non rejetée ; en déduire
les valeurs correspondantes U1 min et U1 max de la tension U
2- L’amplificateur AO1 fonctionne en régime linéaire.
2.1- Donner le nom du montage réalisé autour de cet amplificateur.
2.2- Sachant que R2=10.R1, donner l’expression de U2 en fonction de U1.
2.3- En déduire alors U2 en fonction de la masse M.
2.4- Déterminer l’intervalle [U2min , U2max] de la tension U2 qui correspond à la brioche acceptée.
3- Les amplificateurs opérationnels AO2 et AO3 fonctionnent en commutation et les tensions de seuil VS1
et VS2 sont respectivement égale à 4,95 V et 6,05 V.
3.1- Sachant que R4= 1 KΩ, calculer la valeur du courant I et en déduire les valeurs des résistances R3, et R5 .
3.2- Tracer le graphe U3 en fonction de U2.
3.3- Tracer le graphe U4 en fonction de U2.
3.4- Tracer à partir des deux graphes précédents le graphe U5 en fonction de U2.
3.5- Quelle est la fonction logique réalisée par l’ensemble {D1 , D2 , R6} ?
3.6- Décrire brièvement la fonction réalisée par le bloc C.
SOLUTION
1-masse et tention
M=90g Mmax =110g U1min=0,45 et U1max=0,55
2.1- Nom du montage à AO1 :
Amplificateur non inverseur.
2.2-Tension U2 en fonction de U1 :
U2 = 11.U1
2.3- Tension U2 en fonction de k et M :
U2 = 11.k.M = 55.10-3.M
2.4- Intervalle [U2min ; U2max] de la tension U2 qui correspond à la brioche acceptée :
U2min;U2max=4,95V;6,05
3.1-
I= (VS2 –VS1)/ R4 = 1,1 mA R3 = 5,41 kΩ R5 = 4,5 kΩ
EXERCICE6
Le dispositif de pesage est constitué principalement de capteurs de contrainte pour la détection de la masse m dusable. Le montage de mesure est un pont de Wheatstone ; les amplificateurs opérationnels sont supposés parfaits.
Les résistors R2 et R3 ont des résistances fixes insensibles aux déformations et leur valeur est
R2 = R3 = R = 5 kΩ , tandis que les résistors R0 et R1 sont des capteurs de contrainte de même valeur que R lorsqu’il n’y a aucune masse à mesurer et ils changent de valeur sous l’action de la masse.
Avec ΔR la variation de la résistance R sous l'effet de la masse du sable.
2.1- Exprimer Va en fonction de Vcc , R0 et R1 .
2.2- Montrer que sous l’action d’une masse m du sable :
Va=Vcc.(R+Δ)/2R
2.3- sachant que Vb=Vcc.R3/R2+R3
montrer que sous l’action d’une masse m du sable :
Uab=Vcc/2 . ΔR/R
2.4- Dans la zone linéaire de la caractéristique du capteur, la variation ΔR est proportionnelle à la
masse : ΔR = k0.m k0 est la sensibilité du capteur et on admet que sa valeur est de 2 Ω/Kg.
Exprimer alors la tension Uab(en volt) en fonction de m(en Kg) ; on donne Vcc = 5 V et R = 5 kΩ .
Exprimer alors la tension Uab(en volt) en fonction de m(en Kg) ; on donne Vcc = 5 V et R = 5 kΩ .
2.5- Sachant que les tensions : Ve1 = 3Vb - 2Va et Ve2 = 3Va - 2Vb .
a- En déduire alors l’expression de la tension Vs en fonction de Uab et des éléments du montage
mettre cette expression sous la forme Vs = K.Uab et donner alors l’expression de K
b- Exprimer alors la tension Vs (en volt) en fonction de m (en Kg).
2.6- Quelle est la valeur du rapport R6/R5 pour avoir VS = 5 V correspondant à m = 250 Kg ?
SOLUTION
2.1- Exprimer Va en fonction de Vcc , R0 et R1
Va=Vcc.R1/(R1+R0)
2.2-On remplace R0 par(R - ΔR) et R1 par(R + ΔR), on en déduit que
Va=Vcc.(R+ΔR)/2R
2.3-
Uab= Va – Vb= Vcc.(R+ΔR)/2R - Vcc.R3/(R2+R3) = Vcc.(R+ΔR)/2R - Vcc/2 = Vcc/2. ΔR/R
2.4- Exprimer alors la tension Uab en fonction de m ; on donne Vcc = 5 V.
On trouve que : Uab = 10-3.m
2.5- a- En déduire alors l’expression de la tension Vs en fonction de Uab et des éléments du
montage ; mettre cette expression sous la forme Vs = K.Uab
Vs=5R6/R5 .Uab Vs = K.Uab K=5R6/R5
b- En déduire VS (en volt) en fonction de m (en Kg).
Vs = K.Uab = K=5R6/R5 Uab=10-3. 5R6/R5 .m
2.6- Quelle est la valeur du rapport R6/R5 pour avoir VS = 5 V correspondant à m = 250 Kg ?
R6/R5 =103Vs/5m = 103.5/5.250 =4