La loi des mailles
mailles. Définition d'une maille : Une maille est un chemin fermé, dans un circuit électrique, le long duquel toutes les tensions sont annotées. Cette loi découle de la définition de la tension comme différence de potentiel entre deux points. La tension entre a et b est U = Vb - Va .
On définit une maille comme étant un ensemble de branches d'un circuit qui forme une boucle. Dans une maille, la somme algébrique des tensions le long de la maille est constamment nulle
Loi des nœuds :
La somme des intensités des courants arrivant à un nœud est égale à la somme des intensités des courants sortant du nœud. U représente la tension entre les points A et B ; elle est schématisée par une flèche dont la pointe est tournée vers A
loi d'additivité des tensions : La tension aux bornes d'un ensemble de récepteurs en série est égale à la somme des tensions aux bornes de chaque récepteur. Dans un circuit en série, où les récepteurs sont reliés à un générateur, la somme des tensions de tous les récepteurs est égale à la tension du générateur.
Loi des nœuds : La somme des intensités des courants arrivant à un nœud est égale à la somme des intensités des courants sortant du nœud. U représente la tension entre les points A et B ; elle est schématisée par une flèche dont la pointe est tournée vers A.
Une branche est une partie du circuit électrique située entre deux nœuds consécutifs. Les branches dérivées (ou secondaires) qui ne contiennent que des récepteurs. Un nœud est un point du circuit auquel sont reliés au moins deux bornes de deux dipoles différents
Chaque résistance ajoutée en série dans un circuit augmente la résistance totale du circuit. La forme pour calculer la résistance équivalente à n résistances placées en série est : Req = R1 + R2 +... Rn. C'est tout, les valeurs des résistances placées en série s'additionnent simplement
Loi des mailles
Exercice 1
Soit le schéma suivant :

On donne : UAM = 12V, UBM = 8V, UCM = 6V et UDM = 4V
1. Calculer VA, VB, VC et VD
2. En déduire les tensions UAB, UBC et UCD
1. Calculer VA, VB, VC et VD
2. En déduire les tensions UAB, UBC et UCD
slution
1). VA = UAM = 12V,
VB = UBM = 8V,
VC = VCM = 6V, et
VD =VDM = 4V
2). UAB = VA - VB = 12V - 8V = 4V,
UBC = VB - VC = 8V - 6V = 2V et
UCD = VC - VD = 6V - 4V = 2V
Exercice 2
On considère le circuit du schéma suivant :

Calculer les valeurs des tensions UBD et UAE .
slution
UBD = UB - UD = (UB – UC) + (UC - UD) = 1V + 3V = 4V
UAE =UA – UE = (UA – UB) + (UB - UD) + (UD – UE)= 4V + 4V + 4V = 12V
Exercice 2
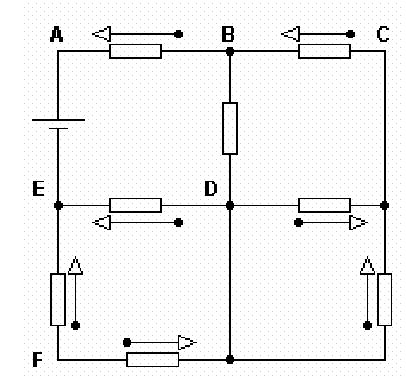
On donne UAB = 8V, UBD = 10V, UED = -6V, UBC = 6V et UDF = 2V
1. Calculer les valeurs de toutes les autres tensions représentées.
2. Si UE = 0, calculer les potentiels de tous les autres points.
1. Calculer les valeurs de toutes les autres tensions représentées.
2. Si UE = 0, calculer les potentiels de tous les autres points.
slution
On donne UAB = 8V, UBD = 10V, UED = -6V, UBC = 6V et UDF = 2V
1) UCD = UC - UD = (UC – UB) + (UB - UD) = - UBC +UBD = - 6V + 10V = 4V
UEF = UE – UF = (UE – UD) + (UD – UD) = UED + UDF = - 6V + 2V = -4V
UAE = UA – UE = (UA – UB) + (UB – UD) + (UD – UE) = UAE + UBD + UDE = 8V + 10V + 6V= 24V
2) Si UE = 0, UAE = UA – UE = UA – 0V = 24V ⇒ UA = 24V UAB = UA – UB= 24V - UB = 8V ⇒ UB = 24V - 8V = 16V UBC = UB – UC = 16V - UC = 6V ⇒ UC = 16V – 6V = 10V UED = UE – UD = 0V - UD = -6V ⇒ UD = 0V – (-6V) = 6V UDF = UD – UF = 6V - UF = 2V ⇒ UF = 6V - 2V = 4V
Exercice 3

slution

I =I1 +I2 + I3
E = + R1I1 = -E2 + R2I2 = -E3 + R3I3
I1 = (E - E1)/ R1 = (10V – 5V) / 1k = 5mA
I2 = (E + E2)/ R2 = (10V + 3V) / 2,2k = 5,91mA
I3 = (E + E3)/ R3 = (10V + 6V) / 3,3k = 4,85mA
I = 5mA + 5,91mA + 4,85mA = 15,76mA
E = + R1I1 = -E2 + R2I2 = -E3 + R3I3
I1 = (E - E1)/ R1 = (10V – 5V) / 1k = 5mA
I2 = (E + E2)/ R2 = (10V + 3V) / 2,2k = 5,91mA
I3 = (E + E3)/ R3 = (10V + 6V) / 3,3k = 4,85mA
I = 5mA + 5,91mA + 4,85mA = 15,76mA
Exercice 4
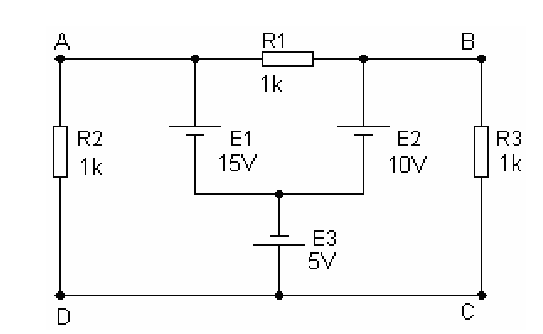
slution
UAD = R2I2 = E1 – E3 = 15V – 5V = 10V ⇒ I2 = 10V / 1k = 10mA
UBC =R3 I3 = E2 – E3 = 10V – 5V = 5V ⇒ I3 = 5V / 1k = 5mA
UAB = UA – UB = (UA – UD) + (UD – UC) + (UC – UB) = 10V + 0V – 5V = 5V
UAB =R1I1 = 5V ⇒ I1 = 5V / 1k = 5mA
UBC =R3 I3 = E2 – E3 = 10V – 5V = 5V ⇒ I3 = 5V / 1k = 5mA
UAB = UA – UB = (UA – UD) + (UD – UC) + (UC – UB) = 10V + 0V – 5V = 5V
UAB =R1I1 = 5V ⇒ I1 = 5V / 1k = 5mA
Exercice 5

Calculer les courants I1, I2 et I3 qui circulent respectivement dans les résistances R1, R2 et R3.
slution
UAD = R2I2 = E1 – E3 = 15V – 5V = 10V ⇒ I2 = 10V / 1k = 10mA
UBC =R3 I3 = E2 – E3 = 10V – 5V = 5V ⇒ I3 = 5V / 1k = 5mA
UAB = UA – UB = (UA – UD) + (UD – UC) + (UC – UB) = 10V + 0V – 5V = 5V
UAB =R1I1 = 5V ⇒ I1 = 5V / 1k = 5mA
UBC =R3 I3 = E2 – E3 = 10V – 5V = 5V ⇒ I3 = 5V / 1k = 5mA
UAB = UA – UB = (UA – UD) + (UD – UC) + (UC – UB) = 10V + 0V – 5V = 5V
UAB =R1I1 = 5V ⇒ I1 = 5V / 1k = 5mA
théorème de Thévenin





loi de Kirchhoff


exercice2

Trouver les courants traversant chacune des résistances. Supposons qu'il n'y a pas de résistance interne de toute alimentation électrique.


On désire calculer :a) la valeur de la résistance équivalente ;
b) le courant fourni par la source ;
c) le courant et la chute de tension dans chacune des résistances ;
d) l'énergie dissipée par chacune des résistances ;
e) la puissance fournie par la source.



Diviseur de tension
Déterminer la tension à travers et
et  en utilisant la règle de division de tension .
en utilisant la règle de division de tension .
Suppose que:
 ,
,  ,
,  ,
,  et
et 


Mais pour le circuit original, l'équation ci-dessus ne sont pas correctes. Pour résoudre le circuit en utilisant leiviseur de tension, nous devons trouver l'équivalent Thevenin du circuit de couleur:
 et
et  sont en série et leur équivalent est égal à
sont en série et leur équivalent est égal à 



exercice1
Utiliser le théorème de Thévenin pour déterminer  .
.

SOLUTION

exercice2
Trouvez les circuits équivalents de Thévenin et Norton:

Supposer que R1=5 ohm, R2=2ohm et Is=2A.
SOLUTION


loi de Kirchhoff
Soit le circuit suivant :

On donne: R1= 1kΩ ,R2= 2kΩ ,R3= 4kΩ ,R4=R5=3kΩ ; a tension aux bornes de la résistance R2 ,UR2= 4v ,et le courant I3= 4mA .
Calculer E et R
solution
exercice2

Trouver les courants traversant chacune des résistances. Supposons qu'il n'y a pas de résistance interne de toute alimentation électrique.
solution

circuits mixtes
exercice1
La figure suivante montre un circuit mixte composé de quatre résistances (R1 = 40 ohms, R2 = 4 ohms, R3 = 10 ohms et R4 = 15 ohms) branchées à une source de tension de 32 V.
La figure suivante montre un circuit mixte composé de quatre résistances (R1 = 40 ohms, R2 = 4 ohms, R3 = 10 ohms et R4 = 15 ohms) branchées à une source de tension de 32 V.

b) le courant fourni par la source ;
c) le courant et la chute de tension dans chacune des résistances ;
d) l'énergie dissipée par chacune des résistances ;
e) la puissance fournie par la source.



Diviseur de tension
Déterminer la tension à travers
Suppose que:

solution
S'il vous plaît noter que la règle de division de tension ne peut pas être appliqué directement. Cela revient à dire que: La raison en est que certains de courant est en passant par  et
et  une succursale. Si la branche a été brisée à un moment donné,
une succursale. Si la branche a été brisée à un moment donné,

nous pourrions appliquer la règle de division de tension et dire
Mais pour le circuit original, l'équation ci-dessus ne sont pas correctes. Pour résoudre le circuit en utilisant leiviseur de tension, nous devons trouver l'équivalent Thevenin du circuit de couleur:
 et
et 
Ainsi, le circuit est simplifié à ce niveau maintenant:

Et la règle de division de tension peut être appliquée directement:
S'il vous plaît noter que

Et la règle de division de tension peut être appliquée directement:
S'il vous plaît noter que  est la tension aux bornes de
est la tension aux bornes de  et la combinaison en série d'
et la combinaison en série d'  et
et  comme indiqué ci-dessous:
comme indiqué ci-dessous:

Maintenant, nous pouvons utiliser la règle de division de tension pour trouver  et
et  . Nous ne pouvons ignorer le reste du circuit et supposer que cette partie est comme suit:
. Nous ne pouvons ignorer le reste du circuit et supposer que cette partie est comme suit:



EXERCICE2

U = 16 V
1.Calculer la résistance équivalente à tout le réseau, vue entre les points A et M.
2.Calculer les tensions VBM, VCM et VDM.
EXERCICE3
Trouver  (ou
(ou  ) et
) et  (ou
(ou  ) En utilisant la règle de division de tension .
) En utilisant la règle de division de tension .

b)

c)

e)

solution

a) Diviseur de tension:  La loi d'Ohm:
La loi d'Ohm: 




c)

Diviseur de tension

La loi d'Ohm:

e)




Diviseur de tension:


